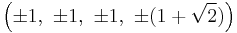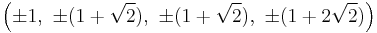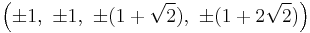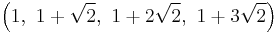Runcinated tesseract

Orthogonal projections in BC₄ Coxeter plane
Tesseract	Runcinated tesseract (Runcinated 16-cell)	16-cell
Runcitruncated tesseract (Runcicantellated 16-cell)	Runcitruncated 16-cell (Runcicantellated tesseract)	Omnitruncated tesseract (Omnitruncated 16-cell)

In four-dimensional geometry, a runcinated tesseract (or runcinated 16-cell) is a convex uniform polychoron, being a runcination (a 3rd order truncation) of the regular tesseract.

There are 4 degrees of runcinations of the tesseract including with permutations truncations and cantellations.

Runcinated tesseract

Runcinated tesseract
Schlegel diagram with 16 tetrahedra
Type	Uniform polychoron
Schläfli symbol	t_0,3{4,3,3}
Coxeter-Dynkin diagrams
Cells	80	16 3.3.3 32 3.4.4 32 4.4.4
Faces	208	64 {3} 144 {4}
Edges	192
Vertices	64
Vertex figure	Equilateral-triangular antipodium
Symmetry group	[3,3,4]
Properties	convex
Uniform index	14 15 16

The runcinated tesseract has 16 tetrahedra, 32 cubes, and 32 triangular prisms. Each vertex is shared by 4 cubes, 3 triangular prisms and one tetrahedron.

Construction

The runcinated tesseract may be constructed by expanding the cells of a tesseract radially, and filling in the gaps with tetrahedra (vertex figures), cubes (face prisms), and triangular prisms (edge figures). The same process applied to a 16-cell also yields the same figure.

Cartesian coordinates

The Cartesian coordinates of the vertices of the runcinated tesseract with edge length 2 are all permutations of:

$\left(\pm 1,\ \pm 1,\ \pm 1,\ \pm(1%2B\sqrt{2})\right)$

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

Schlegel diagrams
Wireframe	Wireframe with 16 tetrahedra.	Wireframe with 32 triangular prisms.

Structure

Eight of the cubical cells are connected to the other 24 cubical cells via all 6 square faces. The other 24 cubical cells are connected to the former 8 cells via only two opposite square faces; the remaining 4 faces are connected to the triangular prisms. The triangular prisms are connected to the tetrahedra via their triangular faces.

Projections

The cube-first orthographic projection of the runcinated tesseract into 3-dimensional space has a (small) rhombicuboctahedral envelope. The images of its cells are laid out within this envelope as follows:

The nearest and farthest cube from the 4d viewpoint projects to a cubical volume in the center of the envelope.
Six cuboidal volumes connect this central cube to the 6 axial square faces of the rhombicuboctahedron. These are the images of 12 of the cubical cells (each pair of cubes share an image).
The 18 square faces of the envelope are the images of the other cubical cells.
The 12 wedge-shaped volumes connecting the edges of the central cube to the non-axial square faces of the envelope are the images of 24 of the triangular prisms (a pair of cells per image).
The 8 triangular faces of the envelope are the images of the remaining 8 triangular prisms.
Finally, the 8 tetrahedral volumes connecting the vertices of the central cube to the triangular faces of the envelope are the images of the 16 tetrahedra (again, a pair of cells per image).

This layout of cells in projection is analogous to the layout of the faces of the (small) rhombicuboctahedron under projection to 2 dimensions. The rhombicuboctahedron is also constructed from the cube or the octahedron in an analogous way to the runcinated tesseract. Hence, the runcinated tesseract may be thought of as the 4-dimensional analogue of the rhombicuboctahedron.

Runcitruncated tesseract

Runcitruncated tesseract
Schlegel diagram centered on a truncated cube, with cuboctahedral cells shown
Type	Uniform polychoron
Schläfli symbol	t_0,1,3{4,3,3}
Coxeter-Dynkin diagrams
Cells	80	8 3.4.4 16 3.4.3.4 24 4.4.8 32 3.4.4
Faces	368	128 {3} 192 {4} 48 {8}
Edges	480
Vertices	192
Vertex figure	Rectangular pyramid
Symmetry group	B₄, [3,3,4]
Properties	convex
Uniform index	18 19 20

The runcitruncated tesseract is bounded by 80 cells: 8 truncated cubes, 16 cuboctahedra, 24 octagonal prisms, and 32 triangular prisms.

Construction

The runcitruncated tesseract may be constructed from the truncated tesseract by expanding the truncated cube cells outward radially, and inserting octagonal prisms between them. In the process, the tetrahedra expand into cuboctahedra, and triangular prisms fill in the remaining gaps.

The Cartesian coordinates of the vertices of the runcitruncated tesseract having an edge length of 2 is given by all permutations of:

$\left(\pm1,\ \pm(1%2B\sqrt{2}),\ \pm(1%2B\sqrt{2}),\ \pm(1%2B2\sqrt{2})\right)$

Projections

In the truncated cube first parallel projection of the runcitruncated tesseract into 3-dimensional space, the projection image is laid out as follows:

The projection envelope is a non-uniform (small) rhombicuboctahedron, with 6 square faces and 12 rectangular faces.
Two of the truncated cube cells project to a truncated cube in the center of the projection envelope.
Six octagonal prisms connect this central truncated cube to the square faces of the envelope. These are the images of 12 of the octahedral prism cells, two cells to each image.
The remaining 12 octahedral prisms are projected to the rectangular faces of the envelope.
The 6 square faces of the envelope are the images of the remaining 6 truncated cube cells.
Twelve right-angle triangular prisms connect the inner octagonal prisms. These are the images of 24 of the triangular prism cells. The remaining 8 triangular prisms project onto the triangular faces of the envelope.
The 8 remaining volumes lying between the triangular faces of the envelope and the inner truncated cube are the images of the 16 cuboctahedral cells, a pair of cells to each image.

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

Stereographic projection with its 128 blue triangular faces and its 192 green quad faces.

Runcitruncated 16-cell

Runcitruncated 16-cell
Schlegel diagrams centered on rhombicuboctahedron and truncated tetrahedron
Type	Uniform polychoron
Schläfli symbol	t_0,1,3{3,3,4}
Coxeter-Dynkin diagram
Cells	80	8 3.4.4.4 16 3.6.6 24 4.4.4 32 4.4.6
Faces	368	64 {3} 240 {4} 64 {6}
Edges	480
Vertices	192
Vertex figure	Trapezoidal pyramid
Symmetry group	B₄, [3,3,4]
Properties	convex
Uniform index	19 20 21

The runcitruncated 16-cell (or runcicantellated tesseract) is bounded by 80 cells: 8 small rhombicuboctahedra, 16 truncated tetrahedra, 24 cubes, and 32 hexagonal prisms.

Construction

The runcitruncated 16-cell may be constructed by contracting the small rhombicuboctahedral cells of the cantellated tesseract radially, and filling in the spaces between them with cubes. In the process, the octahedral cells expand into truncated tetrahedra (half of their triangular faces are expanded into hexagons by pulling apart the edges), and the triangular prisms expand into hexagonal prisms (each with its three original square faces joined, as before, to small rhombicuboctahedra, and its three new square faces joined to cubes).

The vertices of a runcitruncated 16-cell having an edge length of 2 is given by all permutations of the following Cartesian coordinates:

$\left(\pm1,\ \pm1,\ \pm(1%2B\sqrt{2}),\ \pm(1%2B2\sqrt{2})\right)$

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

Structure

The small rhombicuboctahedral cells are joined via their 6 axial square faces to the cubical cells, and joined via their 12 non-axial square faces to the hexagonal prisms. The cubical cells are joined to the rhombicuboctahedra via 2 opposite faces, and joined to the hexagonal prisms via the remaining 4 faces. The hexagonal prisms are connected to the truncated tetrahedra via their hexagonal faces, and to the rhombicuboctahedra via 3 of their square faces each, and to the cubes via the other 3 square faces. The truncated tetrahedra are joined to the rhombicuboctahedra via their triangular faces, and the hexagonal prisms via their hexagonal faces.

Projections

The following is the layout of the cells of the runcitruncated 16-cell under the parallel projection, small rhombicuboctahedron first, into 3-dimensional space:

The projection envelope is a great rhombicuboctahedron.
Six of the small rhombicuboctahedra project onto the 6 octagonal faces of this envelope, and the other two project to a small rhombicuboctahedron lying at the center of this envelope.
The 6 cuboidal volumes connecting the axial square faces of the central small rhombicuboctahedron to the center of the octagons correspond with the image of 12 of the cubical cells (each pair of the twelve share the same image).
The remaining 12 cubical cells project onto the 12 square faces of the great rhombicuboctahedral envelope.
The 8 volumes connecting the hexagons of the envelope to the triangular faces of the central rhombicuboctahedron are the images of the 16 truncated tetrahedra.
The remaining 12 spaces connecting the non-axial square faces of the central small rhombicuboctahedron to the square faces of the envelope are the images of 24 of the hexagonal prisms.
Finally, the last 8 hexagonal prisms project onto the hexagonal faces of the envelope.

This layout of cells is similar to the layout of the faces of the great rhombicuboctahedron under the projection into 2-dimensional space. Hence, the runcitruncated 16-cell may be thought of as one of the 4-dimensional analogues of the great rhombicuboctahedron. The other analogue is the omnitruncated tesseract.

Omnitruncated tesseract

Omnitruncated tesseract
Schlegel diagram, centered on truncated cuboctahedron, truncated octahedral cells shown
Type	Uniform polychoron
Schläfli symbol	t_0,1,2,3{3,3,4}
Coxeter-Dynkin diagrams
Cells	80	8 4.6.8 16 4.6.6 24 4.4.8 32 4.4.6
Faces	464	288 {4} 128 {6} 48 {8}
Edges	768
Vertices	384
Vertex figure	Chiral scalene tetrahedron
Symmetry group	[3,3,4]
Properties	convex
Uniform index	20 21 22

The omnitruncated tesseract (or omnitruncated 16-cell) is bounded by 80 cells: 8 truncated cuboctahedra, 16 truncated octahedra, 24 octagonal prisms, and 32 hexagonal prisms.

Construction

The omnitruncated tesseract can be constructed from the cantitruncated tesseract by radially displacing the truncated cuboctahedral cells so that octagonal prisms can be inserted between their octagonal faces. As a result, the triangular prisms expand into hexagonal prisms, and the truncated tetrahedra expand into truncated octahedra.

The Cartesian coordinates of the vertices of an omnitruncated tesseract having an edge length of 2 are given by all permutations of coordinates and sign of:

$\left(1,\ 1%2B\sqrt{2},\ 1%2B2\sqrt{2},\ 1%2B3\sqrt{2}\right)$

Structure

The truncated cuboctahedra cells are joined to the octagonal prisms via their octagonal faces, the truncated octahedra via their hexagonal faces, and the hexagonal prisms via their square faces. The octagonal prisms are joined to the hexagonal prisms and the truncated octahedra via their square faces, and the hexagonal prisms are joined to the truncated octahedra via their hexagonal faces.

Projections

In the truncated cuboctahedron first parallel projection of the omnitruncated tesseract into 3 dimensions, the images of its cells are laid out as follows:

The projection envelope is in the shape of a non-uniform truncated cuboctahedron.
Two of the truncated cuboctahedra project to the center of the projection envelope.
The remaining 6 truncated cuboctahedra project to the (non-regular) octagonal faces of the envelope. These are connected to the central truncated cuboctahedron via 6 octagonal prisms, which are the images of the octagonal prism cells, a pair to each image.
The 8 hexagonal faces of the envelope are the images of 8 of the hexagonal prisms.
The remaining hexagonal prisms are projected to 12 non-regular hexagonal prism images, lying where a cube's edges would be. Each image corresponds to two cells.
Finally, the 8 volumes between the hexagonal faces of the projection envelope and the hexagonal faces of the central truncated cuboctahedron are the images of the 16 truncated octahedra, two cells to each image.

This layout of cells in projection is similar to that of the runcitruncated 16-cell, which is analogous to the layout of faces in the octagon-first projection of the truncated cuboctahedron into 2 dimensions. Thus, the omnitruncated tesseract may be thought of as another analogue of the truncated cuboctahedron in 4 dimensions.

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

Perspective projections
Perspective projection centered on one of the truncated cuboctahedral cells, highlighted in yellow. Six of the surrounding octahedral prisms rendered in blue, and the remaining cells in green. Cells obscured from 4D viewpoint culled for clarity's sake.	Perspective projection centered on one of the truncated octahedral cells, highlighted in yellow. Four of the surrounding hexagonal prisms are shown in blue, with 4 more truncated octahedra on the other side of these prisms also shown in yellow. Cells obscured from 4D viewpoint culled for clarity's sake. Some of the other hexagonal and octagonal prisms may be discerned from this view as well.
Stereographic projections
Centered on truncated cuboctahedron	Centered on truncated octahedron

Related uniform polytopes

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol	{4,3,3}	t₁{4,3,3}	t_0,1{4,3,3}	t_0,2{4,3,3}	t_0,3{4,3,3}	t_1,2{4,3,3}	t_0,1,2{4,3,3}	t_0,1,3{4,3,3}	t_0,1,2,3{4,3,3}
Schlegel diagram
B₄ Coxeter plane graph

Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol	{3,3,4}	t₁{3,3,4}	t_0,1{3,3,4}	t_0,2{3,3,4}	t_0,3{3,3,4}	t_1,2{3,3,4}	t_0,1,2{3,3,4}	t_0,1,3{3,3,4}	t_0,1,2,3{3,3,4}
Schlegel diagram
B₄ Coxeter plane graph

References

T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Model 15, 19, 20, and 21, George Olshevsky.
http://www.polytope.de/nr17.html
Richard Klitzing, 4D, uniform polytopes (polychora) x3o3o4x - sidpith, x3o3x4x - proh, x3x3o4x - prit


Family	A_n	BC_n	D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square		Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
n-polytopes	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes

Runcinated tesseract

Contents